题意:
有 $n$ 个数字,可以把 $n$ 个数字分成若干组,只有连续的数字才能分成一组,并且一组最多 2 个数字,问你所有组的最大值-最小值的差值最小是多少。
发现组的类别一共 2n 种,排序之后枚举最大值,然后指针移动用线段树维护即可。
线段树维护的信息有些不同:
$t_{p,x,y}$ 表示 $[l+x, r+y]$ 被覆盖,判断可行的条件是 $t_{1,0,0}$ 是否是 true。
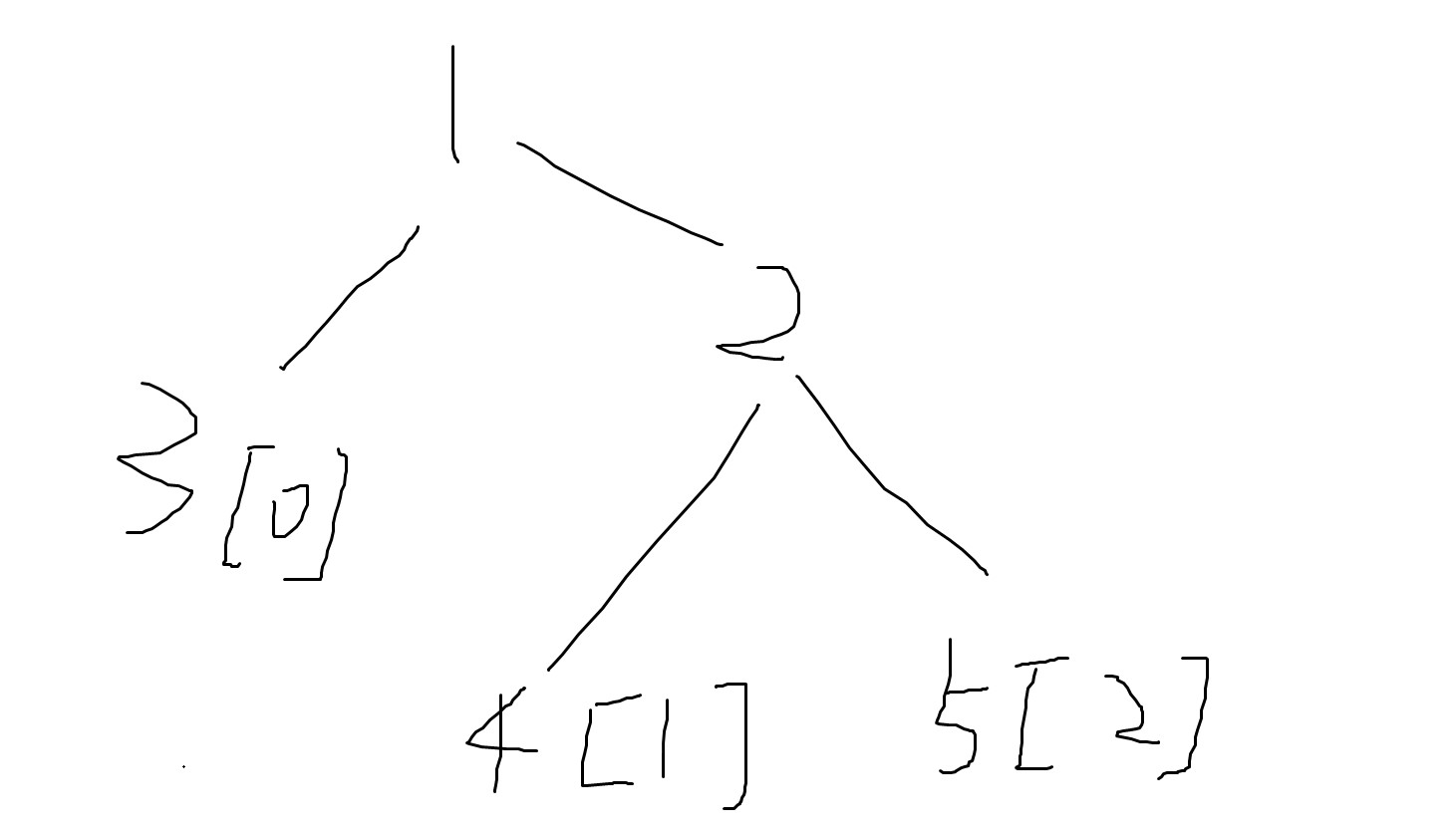
然后发现 $n \times 2$ 大小的 $zkw$ 挂了,原因是可能子树反掉。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
| #include <bits/stdc++.h>
#ifndef LOCAL
#define debug(...) 42
#else
#define debug(...) cerr << "[" << #__VA_ARGS__ << "]:", debug_out(__VA_ARGS__)
#endif
using namespace std;
using ll = long long;
void solve() {
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++)
cin >> a[i];
vector<array<ll, 3>> aa;
for (int i = 0; i < n; i++)
aa.emplace_back(array<ll, 3>{a[i], i, 0});
for (int i = 0; i + 1 < n; i++)
aa.emplace_back(array<ll, 3>{a[i] + a[i + 1], i, 1});
sort(aa.begin(), aa.end());
int L = 0;
while ((1 << L) < n) {
L += 1;
}
int N = 1 << L;
vector<array<array<int, 2>, 2>> t(N * 2);
for (int i = 0; i < n; i++)
t[i + N][1][0] = 1;
for (int i = n; i < N; i++) {
t[i + N][0][0] = 1;
}
auto update = [&](int x) {
for (int i = 0; i < 2; i++)
for (int j = 0; j < 2; j++) {
t[x][i][j] = 0;
for (int k = 0; k < 2; k++)
t[x][i][j] |= t[x * 2][i][k] & t[x * 2 + 1][k][j];
}
};
for (int i = N; i < N + N; i++) {
int x = i;
while (x >>= 1) {
update(x);
}
}
auto upd = [&](int x, int c, bool k) {
x += N;
t[x][0][c] = k;
while (x >>= 1)
update(x);
};
int j = 0;
ll mn = 2e18;
for (int i = 0; i < n * 2 - 1; i++) {
auto [v, x, c] = aa[i];
upd(x, c, 1);
while (t[1][0][0]) {
auto [v2, x2, c2] = aa[j];
mn = min(mn, v - v2);
upd(x2, c2, 0);
j += 1;
}
}
cout << mn << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--)
solve();
return 0;
}
|
