牛客

第一场

rank 15

D

所有后缀的 xor.

注意到任何后缀都可以用前缀和 $S_n - S_i$ 表示。

也就是我们可以用一个 $F(x) = \oplus (x-S_i)$ 来做这个答案。

考虑 $(x - S_i) \mod 2^{k+1}$ 的结果来做讨论 $2^k$ 这一位是 $1$ 还是 $0$。

转化为单点加法，区间求和的问题。

J

考虑两维独立，只有左右边界，那么可以二分到第一个碰壁的位置，然后碰壁和碰壁之间可以倍增求解。

倍增的代码：https://ac.nowcoder.com/acm/contest/view-submission?submissionId=70133770

也可以类似 HoMaMa 一样:https://ac.nowcoder.com/acm/contest/view-submission?submissionId=70123888

struct Fun {
  Int a, b, c, d;
  Int f(Int x) const {
    return min(max(x, a), b) + c;
  } // x = min(max(x, a), b) + c
  Int g(Int x) const {
    return max(x, b) + d;
  } // 从 x 开始顶撞上界的次数，b 是上界，d 是一个常数
  friend Fun operator*(const Fun &p, const Fun &q) {
    const Int a = min(max(q.a - p.c, p.a), p.b);
    const Int b = min(max(q.b - p.c, p.a), p.b);
    const Int c = q.f(p.f(b)) - b;
    const Int d = p.g(b) + q.g(p.f(b)) - b;
    return {a, b, c, d};
  } // 合并信息
  friend std::ostream &operator<<(std::ostream &os, const Fun &p) {
    return os << "(" << p.a << ", " << p.b << "; " << p.c << ", " << p.d << ")";
  }
};
Fun funPlus(Int m, Int t) {
return Fun{0 - t, m - t, t, -(m - t)};
}
Fun funMinus(Int m, Int t) {
return Fun{0 + t, m + t, -t, -(m + t)};
}
constexpr Fun IDENTITY = {-INF, +INF, 0, -INF};

那么维护四颗线段树即可，分别表示上界顶撞次数，下界顶撞次数，两维分别两颗。

第二场

rank 11

A

注意到可以能加就加，加一个，答案至多加 1，也就是加到 $k$ 就直接停下来。

int N,M,K;cin>>N>>M>>K;
  int X,Y;char C;cin>>X>>Y>>C;--X;--Y;
 
  vc<vi>A(N,vi(M,C-'A'));
  int c=(X+Y)&1;if(C=='B')c^=1;
  int ANS=N+M;
  auto check=[&](int i,int j)->int{
    if(0<=i&&i+1<N && 0<=j&&j+1<M){
      return A[i][j]==0 && A[i+1][j]==1 && A[i][j+1]==1 && A[i+1][j+1]==0;
    } else {
      return 0;
    }
  };
  rep(N)rep(j,M){
    A[i][j]=(i+j+c)&1;
    ANS+=check(i-1,j-1);
    if(ANS==K){
      goto here;
    }
  }
  here:
  if(ANS==K){
    cout<<"Yes\n";
    rep(i,N){
      rep(j,M)cout<<char(A[i][j]+'A');
      cout<<"\n";
    }
  }else{
    cout<<"No\n";
  }

B

注意这是一个根号分治，我在开场直接秒了，顺利从 HoMaMa 手里拿到了一血。

当 $k \leq B$ 的时候，使用 $k^2$ 枚举边。

当 $k > B$ 的时候，边数一共有 $m$ 条，直接做一遍就好。

关于根号分治，我暑假的时候写过一个根号数据结构&根号分治.pdf。

第三场

rank 37

A

L

找个中间的 8 填进去，别的全是炸弹，而这样的 8 一定存在。

第四场

rank 4

A

注意到是子树内最深的那个点，先 dfs 在并查集维护一下。

B

注意到人要不经过 $1$ 走到一个 $v$，使得 $(1,v)$ 这条边可以移动到 $(*,n)$，bfs 之后 dij 即可。

C

每次可以对一个四元组排序。

首先考虑，一个序列的环大小。

对于大于等于 $4$ 的环，我们可以容易算出答案。
对于为 $3$ 的环，需要一次。
对于为 $2$ 的环，每两个需要一次。（如果单独多出来还需要）

至此，分类讨论结束。

D

如果一开始一个都不能种，那么已经结束了。
否则一开始种一个 $p$，然后每轮会得到一个 $q$。

那下一次种 $p$ 需要 $\frac{p}{q}$ 的时间，这是上界。

所以大概是 $\sum_{i \geq 1} \frac{p}{q}\times \frac{1}{i} \sim \frac{p}{q} \ln \frac{p}{q}$ 这么多轮会得到每秒 $O(p)$ 的阳光，后面就可以乱种了（因为每秒产出都高于 $p$）预处理一下后缀和即可。

E

注意这个是 $\prod (1 + x^{a_i})$

$\ln(1+x^{a_i}) = \sum_{t=1} (-1)^{t+1}x^{a_it}$

求和之后 exp 即可。

F

注意到链是最大情况，特判奇偶性。

G

略

H

$\gcd_{i=2}^{n}(a_i-a_1)$

I

注意到其实可以预处理出来每个点最左到哪里，类似扫描线一样可以得出答案。

J

题意：有若干个 $0,1,?$，定义权值为 $\sum_{l\leq r} (r-l+1)^k [S_r - S_{l-1}=r-l+1]$ 要求出期望值。

定义一个 $dp_{i,j}$ 表示前 $i$ 个串的 $j$ 次方和，直接二项式定理转移即可，$(1 + x)^{k} = \sum \binom{k}{i}x^i$。

Homama 直接卷积了。https://ac.nowcoder.com/acm/contest/view-submission?submissionId=70419847

这样可以直接算出每一段有多少个长度为 $len$ 的，直接计算 $\sum cnt_{len} \times len^k$。

K

+ 和 * 的表达式求值。

注意 fhq-treap 如果你给数字，符号不同范围的随机值，那么就可以处理优先级。

https://ac.nowcoder.com/acm/contest/view-submission?submissionId=70436416

类似这个

L

简单转化一下题意：可以变成在若干个位置 $\times 2$，在每个位置 $-1$。

然后线段树上二分即可，如果出去了这若干个位置直接输出答案。

第五场

rank 9

A

B

分四种情况讨论。

C

D

E

贪心，相同的前者优先。

F

square-free (3chars) 的一种无限长构造办法是 $parity(i+1)-parity(i)+1$

当然爆搜也很快。

直接做出 $k=0$，然后往里面插入整段即可。（因为本身不含有平方串，所以在跨过的部分也不会有平方串）

G

H

爆搜，复杂度不超过 $3^{n/3}$。

I

J

K

L

M

第六场

rank 6

A

可以使用简单二分来做。

#include <bits/stdc++.h>

using namespace std;
#ifdef DEBUG
#include "debug.hpp"
#else
#define debug(...) (void)0
#endif
using i64 = int64_t;
constexpr i64 mod = 998244353;
int main() {
  cin.tie(nullptr)->sync_with_stdio(false);
  cout << fixed << setprecision(20);
  int t = 1;
  cin >> t;
  for (int ti = 0; ti < t; ti += 1) {
    int n;
    cin >> n;
    vector<vector<pair<int, short>>> adj(n + 1);
    for (int i = 1, x, y, k; i < n; i += 1) {
      cin >> x >> y >> k;
      adj[x].emplace_back(y, k);
      adj[y].emplace_back(x, k);
    }
    vector<int> p(n + 1), o;
    vector<char> odd(n + 1);
    auto rec = [&](auto& rec, int u) -> void {
      for (auto [v, w] : adj[u]) {
        if (v == p[u]) continue;
        p[v] = u;
        odd[v] = odd[u] ^ 1;
        rec(rec, v);
      }
      o.push_back(u);
    };
    rec(rec, 1);
    double l = 0, r = 1;
    for (int _ = 0; _ < 32; _ += 1) {
      double m = (l + r) / 2;
      vector<double> f(n + 1);
      for (int i : o) {
        if (i != 1 and adj[i].size() == 1) continue;
        if (odd[i]) {
          f[i] = 1 / 0.;
          for (auto [j, w] : adj[i])
            if (p[j] == i) f[i] = min(f[i], w - m + min(0., f[j]));
        } else {
          f[i] = -1 / 0.;
          for (auto [j, w] : adj[i])
            if (p[j] == i) f[i] = max(f[i], w - m + min(0., f[j]));
        }
      }
      // debug(m, f);
      if (f[1] >= 0) {
        l = m;
      } else {
        r = m;
      }
    }
    double m = (l + r) / 2;
    cout << m << "\n";
  }
}

B

利用欧拉定理 $V-E+F=2$ 推出来 $n \times \min (k, n - k) + 1$，特判 $n=2k.$

C

首先由于每个点对中有两个点，可以得知 $n \times k$ 必须是偶数。

首先 $k$ 大的时候一定无解。

考虑最终点集的凸包，那么边界上的点在 $< \pi$ 内有 $4$ 个邻居，此时说明有两个相邻邻居会小于 $\pi/3$，一定小于到凸包的距离。
$k=1$ 考虑构造若干平行线段。
$k=2$ 考虑用若干个正多边形构造。
$k=3$ 的结论是 $n \geq 16$ 并且 $n=2k$ 有解。

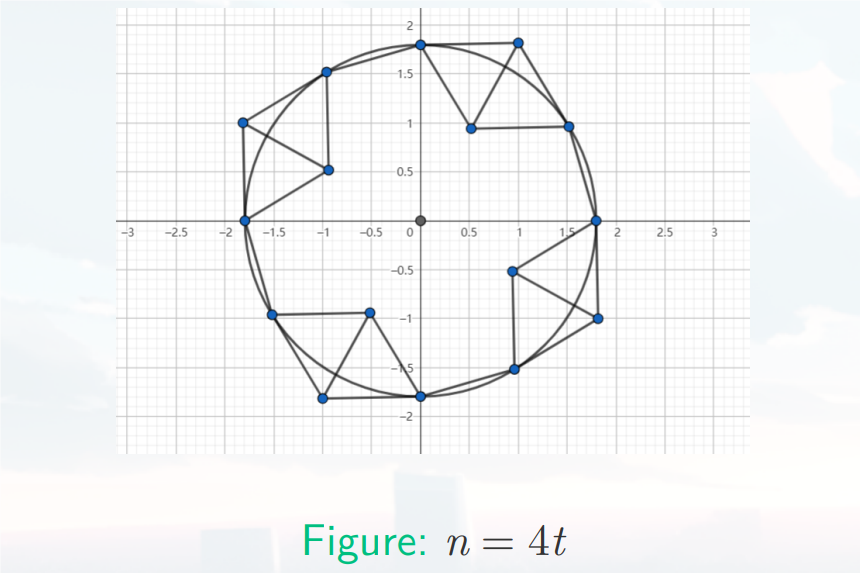
如图两个正三角形可以使得两个点有 $3$ 个邻居，而边界只有 $2$ 个，要去这旁边再构造一个。

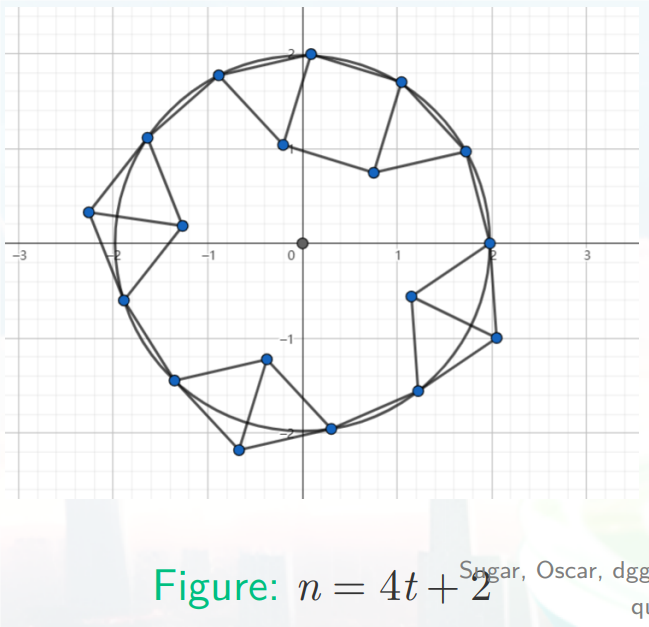
其实和 $4t$ 的情况差不多，难点在于计算。

D

review：边双连通分量的定义：无论删去哪条边，$(u, v)$ 都联通，称 $(u,v)$ 边双连通。

保留所有的黑边，做边双连通分量。然后可以去掉所有的桥边，再使用白边用并查集连起来，看是否连通。

E

求所有长 $n$ 字符集 $k$ 的字符串的本质不同回文子串数量之和。

$n \leq 128, k \leq 10^5.$

还没学会。

F

题意：给一颗森林，求补图的哈密顿路径。

首先不妨假设是一棵树。
如果是菊花，一定不行（这是显然的）

否则可以通过深度分组。

$k \to k+2$ 层之间一定没有边。
同层之间一定没有边。

两个观察就足够做出这题了。

G

给定一个序列，其价值为选择一个合法的括号序列，所有左括号处的数字的和的最大值。现在限制序列的每个数在 $[L_i, R_i]$的实数中均匀随机，求其价值的期望。

$n \leq 100.$

先假设每个数是固定的，肯定是优先队列贪心。
$i = 2k-1$ 的时候必须要选择一个还未被选择的最大数字。

然后这个需要求期望，考虑期望怎么求，对于一个实数序列可以考虑拆掉贡献。

对于 $f(x)$ 来说，可以将 $\leq x$ 的数字看成 $0$，$>x$ 的看成 $1$，然后重复这个答案。

这个序列的最终答案是 $\int_{0}^{\infin} f(x)dx$。

现在 $L_i$ 和 $R_i$ 把实数轴分成若干段，独立计算每一段的 $f(x)$。在每一段，$f(x)$ 都是一个多项式。

假设 $dp_{i,j}$ 表示前 $i$ 个数（$i$ 为奇数），此时优先队列还剩下 $j$ 个 $1$ 的概率多项式。枚举数字是 $0$ 还是 $1$，并且乘上概率。

注意要特判 $L_i=R_i.$

代码待填坑，这个感觉真得写。

H

原神题早该似一似了，在 $S$ 之后添加一个字符 ‘U’ 应该会容易处理一点。

I

给定一个数字矩阵，每一行选择一个区间，要求相邻行的区间有交，最大化选中的数字和。

考虑一个 $f_{i,j}$ 表示考虑了前 $i$ 行，并且选择了 $(i, j)$ 这个位置的最大值。

然后考虑如何更新 $f_{i+1,k}$，其中 $[j,k]/[k,j]$ 必选。

以 $[j,k]$ 为例：

需要一个以 $j$ 结尾的最大连续和。
需要一个以 $k$ 开头的最大连续和。

预处理即可。

J

读题困难.jpg

省流：

如果 $2\dots k$ 的所有编号都有，最后一步一定不能完成。
如果 $\set{2,2}$ 的话，只需一步。

对于其他的情况，一定存在一个编号 $x \in \set{2 \dots k}$ 没有出现的，设为 $x$。

那么显然最后集合个数的操作序列形如 $\set{k(x-1)+1, k \in \mathbb Z}.$

只需要想办法拟合到 $k(x-1)+1$，然后后面一直使用机器 $x$。

事实上只需要使用机器 $y, y = (n-1) \mod (x-1)+1$。（$y$ 堆合成 $1$ 堆。）

K

给定长为 $n$ 的整数序列，分成恰好 $k$ 个非空连续段使得这 $k$ 段的极差之和最小，对 $k = 1 \dots n$ 分别求解。

$n \leq 5000.$

显然有一个状态是 $dp_{i,j}$ 表示把前 $i$ 个分成 $j$ 段的最小值，朴素 $dp$ 是 $O(n^3)$ 的。

但是可以用单调栈维护一下最大最小值，做区间加法，然后线段树查询区间最值，可以做到 $O(n^2 \log n)$，使用 zkw 并标记永久化，感觉可以通过。

upd:真过了，https://ac.nowcoder.com/acm/contest/view-submission?submissionId=70635010

另外值得一提的是，似乎还可以用李超树来维护 $dp_i + cost_{i,j}$，你只需要把 $cost_{i,j}$ 认为是不减的线即可。

学习一下正解。

对于转移代价 $w(l,r’) +w(l’,r) \geq w(l,r) + w(l’,r’)$，对于任意的 $l \leq l’ \leq r’ \leq r$ 成立，满足”反向“四边形不等式。

具体的，对于决策 $p$ 和 $q (p < q)$ 来说：

$dp_{i,j}$ 表示把前 $i$ 个分成 $j$ 段的最小值
$dp_{p-1,k-1} + w(p,j) \leq dp_{q-1,k-1}+w(q,j)$

（暂时还没学太会

appendix.

K 题的原版：https://codeforces.com/gym/103202/problem/L

这题是极差之和的最大值，考虑一个区间 $[l,r]$，肯定存在一个 $i \leq j$，并且 $|A_i - A_j|$ 是他的极差。

然后发现一个事情，$|A_i - A_j| \leq \max\set{A_i - A_j, A_j - A_i}$，这等价于区间内选择两个数，所以会得到一个其他的 $dp$ 方程。

$dp_{i,j,0/1/-1}$。$0$ 表示没有选择，$1$ 表示选择了一个 $+1$ 的系数，$-1$ 表示选择了一个 $-1$ 的系数，也就是消掉一个系数的时候就可以使得段数加 $1$，最后的答案是 $dp_{n,k,0}.$

考虑怎么做 $n \leq 2 \times 10^5.$ 注意到 $+1$ 和 $-1$ 选的个数应该是一样多的，我们考虑把段数的贡献系数放在 $+1$ 上。

$dp[0/1/2][0/1/2][k]$ 分别表示 $[0/+1/-1][0/+1/-1]$ 分了 $k$ 段，而 $+1$ 和 $-1$ 合并，$0$ 和 $0$ 合并，对 $k$ 那一维其实是一个 $\max^+$ 的卷积，而凸函数的 $\max^+$ 卷积可以做到 $O(n)$，$n$ 为当前长度。

所以只需要分治就可以做到 $O(n \log n).$

杭电

第一场

1001~1004 的出题人。

1001 的题解

循环位移这类东西倍长会更加好写。
哈希做法：可以先把 $A$ 的所有本质不同循环位移的哈希值丢进 $\text{map/set}$ 里，然后再依次检查 $B$ 中长度为 $|A|$ 的子串的哈希值是否在 $\text{map/set}$ 里。
后缀数组：考虑直接将 $AA$ 和 $B$ 直接拼起来，检查 $B$ 的子串和排名最相近的的 $AA$ 的子串 $lcp$ 是否大于等于 $|A|$ 即可。

时间复杂度 $O(n \log n).$

1002 的题解

这题有一个 $O(NK)$ 的做法，就是考虑 $dp_{i,j}$ 表示经过前 $i$ 个机会，获得 $j$ 颗星星的最小代价。

下面是正解部分。

正解的思路非常容易&这其实是一个很有意思的问题。
也是优化小体积背包的经典做法。

这题具有一个 $O(N \sqrt K)$ 的做法。

就是首先考虑顺序无关，可以先打乱顺序。

注意到 $N$ 个关卡要获得恰好 $K$ 个星星，那么我们打乱顺序，得到星星的地方是随机并且均匀排布的。（防止被故意构造卡掉）

当选择了前 $i$ 个机会，那么会期望获得 $E = \frac{iK}{N}$ 个星星，而我们只需要在这个期望值附近的一些位置，暴力更新 $dp$ 即可。

本题的体积最大值为 $v=4.$
至于这个区域选择的大小，应当至少是 $B = v \sqrt K$。
我们只需要在 $[E-B,E+B]$ 附近更新 $dp$ 值即可。

所以可以知道复杂度是 $O(N \sqrt K)$ 的。

假设每个地方只有 $0/1$ 颗星星，而非 $0/1/2/3/4$，下面有一组数据可以供大家参考。

下面的是选取 $N,K$ 以及错误率 $\varepsilon$ 所需要的区域大小 $B$。（$K = \frac{N}{2}$ 是错误率最高的时候）

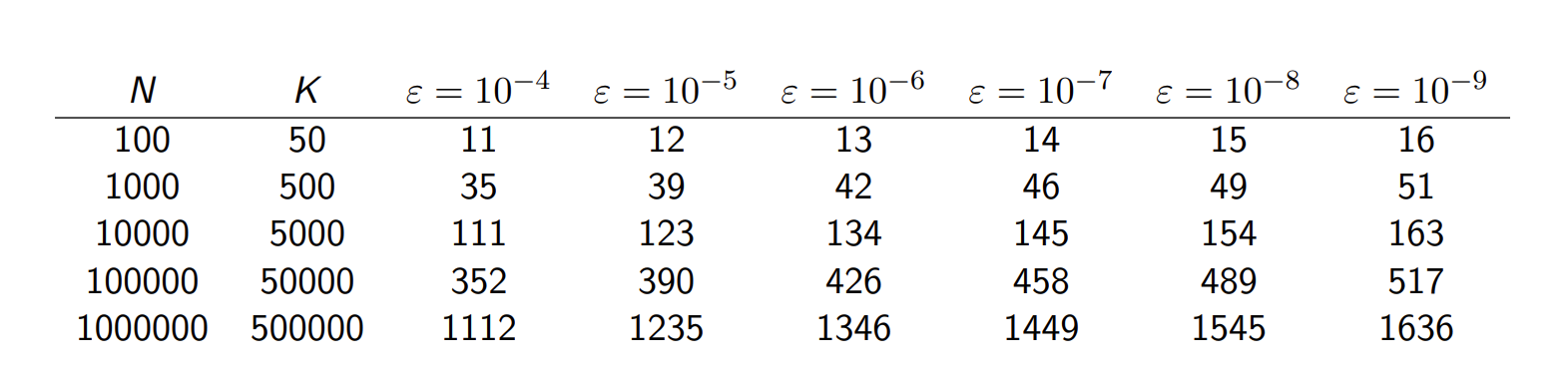
这个数据的来源是：https://arxiv.org/pdf/1309.4029.pdf

1003 的题解

考虑 $\max(a_u, a_v) \times \abs{a_u - a_v}$ 其实是 $\max^2 - \max \times \min$。

由于 $\max \times \min = a_u \times a_v$，这部分是可以简单计算的，答案是：$(\sum_{u \in subtree(i)} a_u)^2$ 。

剩下的问题是 $\sum_{u,v \in subtree(i)} (\max(a_u, a_v))^2$。

对于子树问题，可以想到按照每一条边 $(u, v)$（$v$ 是 $u$ 的某个儿子）依次加入。

具体过程为：

$subtree(u)$ 初始为 ${u}$。
计算 $subtree(v)$ 和当前 $subtree(u)$ 之间点对的答案。（跨越 $u$ 节点的部分）。
把 $subtree(v)$ 子树内的答案直接累加。（不跨越 $u$ 节点的部分）。
$subtree(u) \leftarrow subtree(u) + subtree(v)$（将 $v$ 的子树加入到 $u$ 中）。

对于第四步容易想到启发式合并/线段树合并。

如果采用启发式合并，复杂度是 $O(n \log^2 n)$ 的。如果采用线段树合并，复杂度是 $O(n \log n)$ 的。当然也可以选择 dsu on tree，复杂度 $O(n \log^2 n)$。

1004 的题解

线段树分治+可撤销并查集+lazytag。

并查集是一个树形结构。
线段树分治到叶子结点的时候，对 $1$ 所在的连通块的根节点打上一个 lazytag，表示这一整个子树需要加上一个值。
断开 $(u,v)$ 的话，需要将 $v$ 加上 $u$ 的 lazytag。（假设 $u$ 是 $v$ 的祖先）
如果后续需要连上 $(u,v)$，需要将 $v$ 减掉 $u$ 的 lazytag。（因为 $v$ 在之前时刻不属于 $u$，这是不属于 $v$ 的部分）

第二场

第三场

这场其实没怎么参与，之后要补一下。

1010

使用两次根号分治，还算是一个根号分治的好题。

第四场

1001

三维凸包，但是要特判退化成平面和直线的情况。

1002

学到许多。

可以考虑倒着进行，这样可以不用考虑终态是什么，而初始态已知。
$N=8$ 的图同构本质不同只有$12346$。
图同构可以考虑最小表示。

具体如下：

而这个集合是用哈希加法表示的。

auto msk = [&](ui e) {
    rep(i, N) deg[i] = 0, pt[i] = 0;
    rep(i, N) rep(j, i) {
      if (e >> A[i][j] & 1) {
        q[i][j] = q[j][i] = 1;
        deg[i]++, deg[j]++;
      } else {
        q[i][j] = q[j][i] = 0;
      }
    }
    rep(i, N) {
      pt[i] = qt[i] = 0;
      rep(j, N) {
        if (q[i][j])
          pt[i] += hsh[deg[j]];
      }
    }

  //   ui min_state = LNF;
  //   auto solve = [&](auto &solve, int n, ui s) {
  //     if (n == N) {
  //       ui cur = 0;
  //       rep(i, N) rep(j, i) {
  //         if (q[p[i]][p[j]]) {
  //           cur |= 1uLL << A[i][j];
  //         }
  //       }
  //       if (cur < min_state) {
  //         min_state = cur;
  //       }
  //       return;
  //     }
  //     pair<int, ui> mn = {INF, 0};
  //     rep(i, N) if (~s >> i & 1) {
  //       cmin(mn, make_pair(deg[i], pt[i]));
  //     }
  //     rep(i, N) if (~s >> i & 1) {
  //       if (make_pair(deg[i], pt[i]) == mn) {
  //         p[n] = i;
  //         solve(solve, n + 1, s | (1u << i));
  //       }
  //     }
  //   };
  //   solve(solve, 0, 0);
  //   return min_state; 最小表示

    ui cs = 0;
    rep(i, N) rep(j, i) {
      if (q[i][j]) {
        cs += pt[i] & pt[j];
      }
    }
    rep(i, N) rep(j, i + 1, N) rep(k, j + 1, N) {
      if (q[i][j] && q[i][k] && q[j][k]) {
        cs += pt[i] & pt[j] & pt[k];
      }
    } // 三元环
    rep(i, N) rep(j, N) rep(k, N) rep(l, N) {
      if (q[i][j] && q[j][k] && q[k][l] && q[l][i]) {
        cs += pt[i] & pt[j] & pt[k] & pt[l];
      }
    } // 四元环
    return cs;
  };

  vc<ui> mask;
  auto dfs = [&](auto &dfs, ui e) {
    auto f = msk(e);
    if (mp.count(f)) {
      return mp[f];
    }
    mp[f] = c++;
    mask.pb(e);
    int id = mp[f];
    rep(i, m) if (~e >> i & 1) {
      int v = dfs(dfs, e | (1 << i));
      g[id].pb(v);
      g[v].pb(id);
    }
    return id;
  };
  dfs(dfs, 0);

哈希做法是做好多轮，每轮加上周围一圈的哈希值，复杂度大概是 $O(NM)$ 的。

我的那个做法是数一下度数带权的二元环，三元环，四元环。

（但是其实四元环是 $(a,b,a,b)$ 也没关系，哈希可以乱一点）

对于 $N$ 大的情况，可以考虑矩阵加速，并且只需要奇数和偶数次幂即可，感觉很对。

1003

赛时秒了。只需要考虑素数密度以及答案不减，就可以很快通过，复杂度 $O(n \log n \log V)$，而 $V = O(|A_i| \sqrt N)$。

1004

$4 = 2 + 2.$

钦定 $a_1$ 属于某边集合，这样可以减少一半的状态。
然后爆搜的时候使用 $01$ 背包。
爆搜的复杂度是 $O(2^n)$，$01$ 背包的复杂度是 $O(2^m)$，统计答案的时候也是 $O(2^m)$ 的而钦定了一个，复杂度是 $O(2^{n+m-1})$ 的。

void dfs(int x,int suml,int sumr){
  if(x==n){
    for(int i=0,ml=-1,mr=-1;i<1<<m;i++){
      int o=q[i];
      if(fl[n][o]&&w[o]>=w[o^suml]){
        umax(ml,w[o^suml]);
        if(~mr)umin(ans,w[o]-min(w[o^suml],mr));
      }
      if(fr[n][o]&&w[o]>=w[o^sumr]){
        umax(mr,w[o^sumr]);
        if(~ml)umin(ans,w[o]-min(w[o^sumr],ml));
      }
    }
    return;
  }
  int v=val[x];
  for(int i=0;i<1<<m;i++){
    fl[x+1][i]=fl[x][i]|fl[x][i^v];
    fr[x+1][i]=fr[x][i];
  }
  dfs(x+1,suml^v,sumr);
  for(int i=0;i<1<<m;i++){
    fl[x+1][i]=fl[x][i];
    fr[x+1][i]=fr[x][i]|fr[x][i^v];
  }
  dfs(x+1,suml,sumr^v);
}

1005

签到模拟题。

1006

也许具有意义的 $dp$ 题。

这种转化方式可以减少状态数。

1007

随机题，做法多样。

可以考虑暴力做 $O(\sqrt n \log n)$ 次，这样几乎所有的数字都是 $B$ 中的前 $O(\sqrt n \log n)$ 大的了。这样复杂度是 $O(n \sqrt n \log n)$ 的，常数比较小，亲测取 $B = 3000$ 是合适的。
直接记录最小值，只更新最小值以上的 $B$，这样也可以通过，和做法一本质相同，但是更加好写（可能常数会更大一点）

1008

1009

简单签到。

1010

感觉很牛的想法，$\gcd$ 是容易观察出来的，别的好像不太能观察出来，

1011

有空再实现一下。

1012

扫描线板子题。

第五场

1001

题面。

$2n+1$ 是一个奇数，只考虑 $1,2$ 的性质，假设最后的异或和是 $x$，我只需要全局 $\oplus x$ 就可以做到异或和为零，也就是只需要除掉 $2^{k}$ 即可。
接下来考虑每行每列的限制，可以先填好第二行，方案数是 $2^k$ 的 $n+1$ 次下降幂！
假设集合 $U = \set{1\dots n}$
设 $f(S)$ 为仅有 $S$ 这些位置相同，$g(S)$ 为 $S$ 这些位置相同。
那么我们只需要求解 $f(\empty)$ 即可。
注意到容斥原理是 $f(S) = \sum_{S \subset T} (-1)^{|S|-|T|}g(T)$

那么本题可以做到 $O(n)$ 处理答案。

1002

注意答案只可能是 $\set{n-1,n,n+1}$。

$n-1$ 是容易判断的。
$n$ 需要先操作一次，然后去用 $n-1$ 判断，或者先操作次再暴力。
剩下都是 $n+1$ 次。

1003

1004

注意到 $lcm(i,j) \leq N(N\leq 10^5)$ 只有 $2 \times 10^6$ 对。

离线下来做 dfn 的子树和即可。

1005

只需要对树链的并取 $\max$ 就行，而树链的并可以通过 $v_i \to lca(v_1\dots v_n)$ 这些路径求出。

倒序枚举 $\gcd$，就变成覆盖的问题了，并查集暴力跳即可。

1006

假设 $g=\gcd(a,b,c)$

结论是 $a/g,b/g,c/g$ 的奇偶性相同是 NO，否则 YES。

最终情况显然是 $1,1,1$

观察奇偶性，发现奇数奇数偶数/奇数偶数偶数都能转移到奇数奇数奇数，而奇数奇数奇数只能转到奇数奇数偶数。

按照这种推理下去可以知道胜负。

1007

1008

最大权值闭合子图模型。https://www.cnblogs.com/kikokiko/p/12996168.html

从简单角度入手，选择一条 $(a,b)$ 相当于 $a$ 和 $b$ 在第一棵树都选，并且在第二棵树都不选。

对第一棵树边 $w$ 建立一个点 $z$，我们只需要建立 $s \to^w z \to^{\infin} a$ 以及 $s \to^w z \to^{\infin}b$ 即可。

对第二棵树边 $w$ 新建一个点 $z$，我们只需要建立 $a \to^{\infin} z \to^{w} t$ 以及 $b \to^{\infin} z \to^{w} t$ 即可。

这么建边就做完了。

1009

注意到只需要考虑 $\mu(k) \neq 0$ 的情况，也就是说 $k$ 没有平方因子。

观察：

如果 $k \mid a$，那么 $a^{\varphi(k)+1} \mod k = 0$
否则 $a^{\varphi(k)+1} = a^{0+1} \mod k$

原式 $\sum \mu(k) \times (a^{\varphi(k)+1} \mod k) = \sum \mu(k) \times (a \mod k)$

注意这个可以整除分块，也就是把 $\mod k$ 展开。

得到一个 $a \sum_{k=1} \mu(k) - \sum_{k=1} \mu(k) k \times \lfloor \frac{a}{k} \rfloor$

剩下的部分就可以杜教筛了。

1010

相当于每次查询从 $root \to x$ 选，暴力往下做。

注意到可以树链剖分，只会拆成 $\log$ 条链，也就是说可以对这 $\log$ 条链维护一个指针，表示删到哪里了，就可以做完了。

复杂度是 $O(q \log n + n +q)$ 的，因为每个点最多被删一次，每个 $q$ 最多停止一次。

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
vector<int> G[N];
int sz[N], fa[N], son[N], top[N], dfn[N], d[N], rev[N];
int idx;
void dfs(int u, int p) {
  sz[u] = 1;
  for (auto v : G[u])
    if (v != p) {
      fa[v] = u;
      d[v] = d[u] + 1;
      dfs(v, u), sz[u] += sz[v];
      if (son[u] == -1 || sz[v] > sz[son[u]])
        son[u] = v;
    }
}
void dfs2(int u, int t) {
  top[u] = t, dfn[u] = idx++;
  rev[dfn[u]] = u;
  if (son[u] != -1)
    dfs2(son[u], t);
  for (auto v : G[u])
    if (top[v] == -1)
      dfs2(v, v);
}
int lca(int x, int y) {
  while (top[x] != top[y]) {
    if (d[top[x]] < d[top[y]])
      swap(x, y);
    x = fa[top[x]];
  }
  return d[x] < d[y] ? x : y;
}
vector<pair<int, int>> chain(int x, int y) {
  vector<pair<int, int>> L, R;
  while (top[x] != top[y]) {
    if (d[top[x]] > d[top[y]]) {
      L.emplace_back(dfn[x], dfn[top[x]]);
      x = fa[top[x]];
    } else {
      R.emplace_back(dfn[top[y]], dfn[y]);
      y = fa[top[y]];
    }
  }
  L.emplace_back(dfn[x], dfn[y]);
  reverse(R.begin(), R.end());
  L.insert(L.end(), R.begin(), R.end());
  return L;
}

int p[N], w[N], ptr[N];
void solve(){
  memset(top, -1, sizeof top);
  memset(son, -1, sizeof son);
  idx = 0;
  for (int i = 0; i < N; i++) G[i].clear();
  for (int i = 0; i < N; i++) p[i] = w[i] = ptr[i] = 0;
  int Q, p0, w0; cin >> Q >> p0 >> w0;
  p[0] = p0;
  w[0] = w0;
  vector<array<int, 3>> ops;
  for (int i = 0; i < Q; i++) {
    int op; cin >> op;
    if (op == 1) {
      int u, v, pu, wu; cin >> u >> v >> pu >> wu;
      G[v].push_back(u);
      p[u] = pu;
      w[u] = wu;
    } else if (op == 2) {
      int k, s;
      cin >> k >> s;
      ops.push_back({2, k, s});
    } else {
      int l; cin >> l;
      ops.push_back({3, l, 0});
    }
  }
  dfs(0, -1);
  dfs2(0, 0);
  for (auto [op, k, s] : ops) {
    if (op == 2) {
      auto v = chain(0, k);
      long long ans1 = 0;
      long long ans2 = 0;
      for (auto [l, r] : v) {
        if (ptr[l] < l) {
          ptr[l] = l;
        }
        while (ptr[l] <= r) {
          int u = rev[ptr[l]];
          // cout << u << " " << w[u] << " " << p[u] << "\n";
          if (s >= w[u]) {
            ans1 += w[u];
            ans2 += 1ll * w[u] * p[u];
            s -= w[u];
            w[u] = 0;
          } else {
            ans1 += s;
            ans2 += 1ll * s * p[u];
            w[u] -= s;
            s = 0;
            break;
          }
          ptr[l]++;
        }
        if (s == 0) {
          break;
        }
      }
      cout << ans1 << " " << ans2 << "\n";
    } else {
      w[k] = 0;
    }
  }
}

int main(){
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  int T;
  cin >> T;
  while (T--) {
    solve();
  }
  return 0;
}

注意到其实甚至可以做到单点修改和强制在线。

如果只有单点修改的话可以用并查集缩段，这是很常见的办法，在同一场也使用过这个办法，当然也可以使用 fast_set，也就是压位 trie 来实现这个东西。
对于强制在线和单点修改同时存在的情况，那可能得考虑倍增到最近的那个非 $0$ 点。

1011

$n \equiv 2 (\mod 3)$，答案是 $2^{n-1}$
otherwise, $2^n$

1012

1013

对于 $0$ 号格子有 $\frac{1}{n}$ 的概率走到终点。

对于另外 $\frac{n-1}{n}$ 概率，可以发现概率期望都是相同的，都是 $\frac{1}{n-1}$。

也就是期望步数是 $1 + \frac{(n-1)^2}{n}$。