• 线性基通常指 $\mathbb{Z}_{2}^{n}$ 下的一组线性无关的向量，而向量用二进制数简易表示。
  • 加法相当于异或运算。
  • 内积，两个数各个位相乘再累加，等价于 $\text{parity(u & v)}$，如果该值为 0，则 $u,v$ 正交。
  • $\text{span}(A)$ 里的任何一个数字可以被表示出来 $2^{n-|A|}$ 次。

满足分配律，即 $(u + v)·w = u·w+v·w$。

线性基求交的部分内容。（From Sooke。）

  • 高斯消元：针对线性基的高斯消元，目的在于使各个基的最高一位被各自独占，其余位均为 0，可以解决线性基第 $k$ 大等问题，这些位被称为关键位，其余被称为非关键位。
  • 集合幂级数：集合幂级数可以简单理解成 $[x^u]$ 指标为 $u$ 在 $\mathbb{Z}_{2}^{n}$ 下的向量，二进制数的多项式。
  • 对于集合幂级数 $F$，$\hat F = FWT[F]$，对于 $F$ 的 $[x^u]$，若 $u, w$ 正交，则对 $\hat F$ 的 $[x^w]$ 贡献为正，否则为负，系数即为 $(-1)^{\text{parity(u & w)}}$​。

(定义 $\oplus$ 为 $\text{parity}$ 运算)
$$
fwt[a] \times fwt[b] = \left(\sum_{i\otimes j = 0} a_j - \sum_{i\otimes j = 1} a_j\right)\left(\sum_{i\otimes k = 0} b_k - \sum_{i\otimes k = 1} b_k\right) \
=\left(\sum_{i\otimes j=0}a_j\right)\left(\sum_{i\otimes k=0}b_k\right)-\left(\sum_{i\otimes j=0}a_j\right)\left(\sum_{i\otimes k=1}b_k\right)-\left(\sum_{i\otimes j=1}a_j\right)\left(\sum_{i\otimes k=0}b_k\right)+\left(\sum_{i\otimes j=1}a_j\right)\left(\sum_{i\otimes k=1}b_k\right) \
=\sum_{i\otimes(j \operatorname{xor} k)=0}a_jb_k-\sum_{i\otimes(j\operatorname{xor} k)=1}a_jb_k \
= fwt[c]
$$

$$
\begin{aligned}
fwt[a] &= \text{merge}(fwt[a_0] + fwt[a_1], fwt[a_0] - fwt[a_1]) \\
a &= \text{merge}(\frac{a_0 + a_1}2, \frac{a_0 - a_1}2)
\end{aligned}
$$

求 $F$ 和 $G$ 的 xor 卷积 $H$ 的时候，我们对 $\hat F, \hat G$ 逐项相乘，得到 $\hat H$ 的本质是什么呢？考察 $[x^u] F$ 和 $[x^v]G$ 变换到 $[x^w]H$ 相乘的情形，由分配律，新系数为 $(-1)^{u·w} \times (-1)^{v·w} = (-1)^{(u+v)·w}$,恰好对应 $[x^{u+v}]$ 到 $[x^w]$ 的系数。

与原线性基相反，正交线性基的各个基一般按最低 $1$ 位存储。
正交线性基的构造十分简单，先对 $A$ 高斯消元得到 $k$ 个关键位，$A^{\perp}$ 的 $n-k$ 个正交基各自独占 $n-k$ 个非关键位的 $1$，其中最低 $1$ 位为第 $i$ 位的正交基第 $j$ 位为 $1$ 当且仅当最高 $1$ 位为第 $j$ 位的原始基第 $i$ 位为 $1$，类似转置。一种可行实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// Fennec's Algorithm
for (int i = n - 1; i >= 0; i--) {
    for (int j = i - 1; j >= 0; j--) {
        if (A[i] >> j & 1) { A[i] ^= A[j]; }
    }
}
for (int i = n - 1; i >= 0; i--) {
    if (A[i] == 0) {
        B[i] = 1 << i;
        for (int j = n - 1; j > i; j--) {
            if (A[j] >> i & 1) { B[i] |= 1 << j; }
        }
    }
}

img

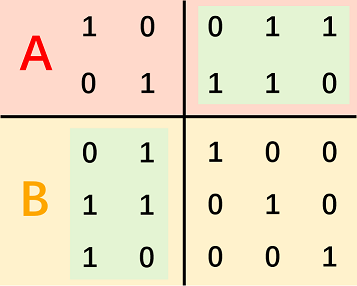
封闭判断。

判断 ${A}$ 是否是一个大小为 $n$ 的线性基构成的。（是否封闭）

排序后判断 $A[i] == A[i - lowbit(i)]\oplus A[lowbit(i)]$。

$A$ 的下标 $[0…2^{n})$。

1336E2

  • $F(S) = \sum_{x \in \text{span}(S)} z^x$。
  • $P(S) = \sum_{x \in \text{span}(x)}z^{popcount(x)}$

对于 $x \in \text{span}(A)$ 来说，$(z^x) * F(A) = F(A)$

那么可以知道

  • $F(A) * F(A) = F(A) \times 2^{rank(A)}$
  • $FWT(F(A)) \times FWT(F(A)) = FWT(F(A)) \times 2^{\text{rank}(A)}$

$x^2 = x\times 2^{\text{rank}(A)}$，仅有两种可能 $x_1 = 0, x_2 = 2^{\text{rank}(A)}$

所以 $[z^i]FWT(F(A)) \in {0, 2^{\text{rank}(A)}}$。

$[z^i] FWT(F(A)) = \sum_{x \in span(A)}(-1)^{\text{popcount(i, x)}} \in {0, 2^{\text{rank(A)}}}$

如果存在 $x$ 使得 $(-1)^{\text{popcount(i, x)}} = -1$，那么 $[z^i]FWT(A) = 0$

定义线性基 $A$ 的正交线性基为 $B$，那么对于所有 $x\in span(A), y \in span(B)$，一定有 $\text{popcount(x and y)}$ 为偶数，即正交定义。